Tutti noi appassionati di allenamento con i pesi abbiamo sentito parlare di curve fisiologiche, i più appassionati avranno sentito parlare anche di biomeccanica della colonna vertebrale, e di come quest’ultime impattino la “resistenza” della colonna.
Iniziamo l’articolo facendo chiarezza su un punto:
Esiste un calcolo facile per valutare la resistenza della colonna (R) alle forze di compressione, ed è l’indice che descrive Kapanji: R = N2+1.
La capacità di sopportazione (R) è data dal numero delle curve alla seconda più uno:

Le normali 3 curve (cervicale, dorsale, lombare) danno un indice di 10 = (32+1).
2 curve danno un indice di 5 = (22+1), la metà.
1 curva dà un indice di 2 = (12+1).
Pertanto, appiattire le curve del rachide equivale e dimezzare la sua capacità di carico.
A chiunque si interessi almeno un po’ di fitness è capitato di imbattersi in questa semplice formula, che sembrerebbe spiegare la natura della forma della colonna vertebrale. Quando, tanti anni fa, lessi questa roba, la mia reazione fu qualcosa del genere:

Da dov’è uscita questa formula? Perché, nonostante le mie conoscenze ingegneristiche, non riuscivo a capire da dove venisse? Curvature limite del modello trave con qualche ipotesi che mi eliminasse la resistenza del materiale? Niente da fare: non ci arrivavo. Così, ho lasciato perdere e mi sono fidato di un ipotetico genio che aveva trovato correlazioni che non vedevo. Dopotutto chi ero io, se non un semplice studente di ingegneria civile?
Passano gli anni e, di tanto in tanto, in qualche discussione Facebook salta fuori qualcosa che mi riporta alla ricerca della fonte di questa formula… ma senza fortuna. Nessuna traccia prima della sua apparizione nel libro del Kapanji, dove peraltro è buttata lì senza spiegazioni. Ma poi, un giorno, leggo un passaggio che mi lascia folgorato:

“deriva dall’instabilità di Eulero”
Il tempo di sbattere le palpebre e tutto si fa cristallino. Finalmente sapevo perché il mio cervello limitato non vedeva là dove era più ovvio guardare.
Purtroppo non ricordo dove ho trovato questa frase. È passato troppo tempo ed è solo colpa di Paolo Evangelista se sto scrivendo questo articolo. Ma da quel preciso momento ho smesso di leggere di stabilità della colonna: l’unica formula che destava in me un qualche interesse era la più sbagliata di tutte. Le altre trattazioni pseudomeccaniche che giravano prendevano cose a caso, tipo il principio degli archi, per applicarle (col culo) alla colonna vertebrale – per non parlare di forze follower che magicamente compaiono all’interno della colonna.
Ci sono vari errori in questa formula. Procediamo con ordine.
Il primo è proprio quello che mi impediva di associare l’instabilità di Eulero a questa formula, anche se era facile:
“…consente di valutare la resistenza della colonna…”
Per molti, la parola resistenza potrebbe non sembrare un errore; ma, per un ingegnere, associare questa parola a quello che segue è profondamente sbagliato.
Quando parliamo di resistenza di una struttura o di un elemento ci riferiamo alla condizione in cui questo, soggetto a delle forze, si rompe o si plasticizza. Lo stesso accade nel parlato comune: se dico di un oggetto che è molto resistente, intendo dire che anche se lo sottoponessi a grandi forze non dovrei buttarlo o ripararlo.
L’instabilità di Eulero, invece, studia il comportamento elastico di una struttura senza considerare quando si rompe; per esempio, come si deforma una trave deformabile soggetta a dei carichi. Il parametro che sta alla base di questo fenomeno è la rigidezza, cioè ciò che determina come si deforma una struttura se soggetta a dei carichi. Nel parlato comune, ciò che spiega perché più un oggetto è rigido più sarà difficile deformarlo.
Questa differenza è ciò che mi impediva di vedere il collegamento, perché mi spingeva a cercare formule o concetti da associare alla resistenza e non alla rigidezza di una struttura. In buona fede, pensavo che fosse quantomeno corretta la premessa teorica di ciò che vuole indicare questo indice. Invece mi sbagliavo.
Bene. Fin qui abbiamo appurato che non si parla di quanto resiste la colonna, ma di come si deforma sotto carico (o almeno questo è quello che vorrebbe fare la formuletta semplice semplice). Il problema è che ci sono altri errori che si vedono solo se si parte dalla fonte. Perciò, bando alle ciance e rifacciamo quello che Eulero fece nel lontano 1755.
Eulero idealizzò il problema di un’asta elastica con una certa rigidezza flessionale e la sua deformazione a partire da certe ipotesi (inestensibilità, deformata a taglio nulla e le sezioni ruotano-traslano ma si mantengono piane).

Arrivando alla definizione del potenziale dell’asta inflessa:

con
E = modulo elastico del materiale
J = inerzia della sezione
L = lunghezza trave
V = potenziale
w = spostamento perpendicolare all’asse funzione della posizione x
Visto che da usare è uno schifo (si può fare… ma anche no!), l’alternativa è lo sviluppo in serie di Taylor, che con un bel po’ di passaggi matematici porta alla semplicissima equazione differenziale:
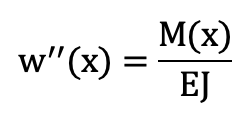
Relazione curvatura momento flettente
M è il momento flettente applicato lungo l’asse della trave, e w’’ è la curvatura che si ha nel punto di coordinate x.
Con questa equazione si risolvono un sacco di problemi. Ancora oggi viene usata per progettare molte strutture: dalla mensola di casa vostra a cose molto grandi, come i ponti.
Per le strutture isostatiche è di una semplicità assoluta, perché basta calcolare il momento flettente dalla configurazione di equilibrio e, integrando la soluzione un paio di volte mettendo le condizioni di vincolo, si ottiene la forma della deformata della trave inflessa. Questo è ciò che è stato fatto per calcolare la flessione del bilanciere nell’articolo sullo stacco da terra e quanto aiuta un bilanciere flessibile o meno.
Ma questa semplicità ha dei limiti. Ci sono casi di travi per le quali il momento flettente è nullo e quindi, secondo questo modello semplificato, non si hanno deformazioni. Questo potrebbe anche essere accettabile: pensate alle gambe del vostro tavolo, se ci poggiate un peso sopra non si flettono, restano rettilinee. Questo, però, è vero fino a un certo carico. Prendete uno stuzzicadenti o un ferro da calza e mettetelo verticale, dopodiché spingete con il dito verso il basso, caricandolo solo assialmente. Fino a un certo carico, resterà bello rettilineo; poi, raggiunta una certa pressione, bam! sbanda da un lato.

Per calcolare questo effetto dobbiamo per forza aggiungere qualche termine dello sviluppo in serie che abbiamo fatto prima. In particolare, dobbiamo arrivare al secondo ordine; quello che si farà poi, infatti, è comunemente chiamata analisi del secondo ordine.
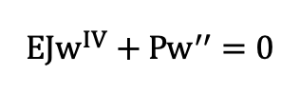
Facciamola breve. Bisogna risolvere questa equazione differenziale mettendo le condizioni al contorno del nostro caso e vedere che cosa esce. Per fortuna ci sono i matematici che ci danno la formula generale della soluzione, con α = P / EJ

È da qui che è stata tirata fuori (per dirla in termini generosi) la formula da cui siamo partiti. Quello che hanno fatto è applicarla al caso in cui il vincolo della trave sia un incastro alla base.

Con questa, la soluzione non banale al problema è:

Questa formula rappresenta tutti i carichi critici dell’asta inflessa, e ad ognuno di essi è associata la deformata corrispondente:

Ciò che ha fatto l’inventore della formuletta iniziale è tagliare la parte costante e tenere solo quella variabile, ovvero il parametro n, che può essere associato al numero di curvature che ha la configurazione deformata associata al carico critico n, semplificandola tanto per dare numeri tondi che alla fine è sempre una parabola:

Abbiamo ripercorso dall’origine la nascita della formula e ora sappiamo dire come l’hanno ottenuta. Ma resta ancora un dubbio: cosa c’è di sbagliato? Quello che abbiamo trovato con tutto questo caos di nozioni matematiche sono tante configurazioni di equilibrio, ma gli autori (Eulero sì, pace all’anima sua) non si sono chiesti se queste siano stabili o meno. Il solito problema della pallina in fondo a una valle o in cima a una collina: entrambe sono posizioni di equilibrio, ma una è stabile e l’altra no.

Lasciamo perdere il procedimento necessario a calcolare la stabilità di una configurazione di equilibrio. Quello che risulta praticamente sempre (forze follower a parte) è che solo il primo carico critico è stabile.
Questo vuol dire che, se provate a fare questo esperimento, non troverete mai n=1, n=2, eccetera, perché raggiunto il primo carico la trave si deforma e… fine dei giochi! Tornando al ferro da calza, risulterebbe questo:

Provate a trovare la configurazione a destra premendo solo con il dito, ovvero applicando la forza P che sia maggiore di PCR(n=2). Scoprirete che è impossibile riuscirci. Il video mostra che anche partendo con un’asta già configurata in questo modo, una volta sottoposta la struttura ad un carico che la deforma, ci troveremo comunque nella configurazione di sinistra.
Bene, abbiamo trovato che l’errore era nel titolo: la formula rappresenta delle configurazioni che non si possono raggiungere. Ma ci sono altri errori? Certo che sì.
Se si fanno tutti questi pipponi matematici è per riuscire a modellare un problema fisico, quindi la matematica deve rappresentare quello che le evidenze mostrano. Il passaggio più difficile è proprio trovare la rappresentazione matematica che meglio descriva la realtà. Nel nostro caso, anche questo è concettualmente sbagliato, e per accorgercene basta buttare dentro qualche valore alla formula del carico critico e vedere cosa esce.
L = lunghezza colonna vertebrale = 500 mm
D = diametro disco vertebrale = 50 mm
J = inerzia disco vertebrale =
E = Modulo elastico disco vertebrale = 10 N/mm2

La colonna vertebrale raggiunge il suo carico critico a circa 3 kg: un valore troppo basso, che ne dite? Cioè, uno che fa stacco con 60kg dovrebbe piegarsi peggio che mai, dal momento che il carico sarebbe 20 volte il carico critico che ci dice quando l’asta verticale sbanda sotto il carico. Come sappiamo, in realtà si vedono addirittura prestazioni con 500kg di stacco, e la schiena mica si flette così tanto.
Com’è possibile? Il modello dà risultati a caso? Così si è preso a parlare di stabilità della colonna nel mondo della biomeccanica. Non perché l’evidenza mostrava l’instabilità nella schiena, ma perché un modello sosteneva questa teoria. Bah, a me queste cose non piacciono molto: se non vedo il riscontro oggettivo, forse sarebbe meglio approfondire cosa diavolo ho calcolato…
Dov’è l’inghippo?
Facciamo un bell’esperimento. Andate dal vostro chirurgo di fiducia (se ne avete uno, vi auguro di no) e fatevi incidere la schiena per tutta la sua lunghezza, recidete tutti i muscoli, i tendini, ecc. dalla colonna vertebrale ed estraetela dalla sua sede: dopodiché, fate lo stesso giochino del ferro da calza. Quello che vedrete è che, con pochi kg, la colonna vertebrale sbanderà… proprio come aveva predetto il buon Eulero!
Quindi il modello è confermato? O, forse, stiamo facendo una minchiata? Voi che dite?
Mentre vi fate rimettere al suo posto la colonna vertebrale (tranquilli, non si è rotta: è sufficientemente resistente), vi faccio un altro esempio con una struttura civile.
Prendiamo i dati di un pilastro del WTC, le Torri Gemelle, e calcoliamo il carico critico:
L = altezza pilastro = 400000 mm
J = inerzia sezione del pilastro = 1,15e12 mm4
E = Modulo elastico acciaio = 210000 N/mm2

Il pilastro si instabilizza con circa 37 ton, peccato che il suo stesso peso supera le 1000 ton… Scacco matto, complottisti! Le torri non sono state fatte saltare: dovevano crollare prima ancora che finissero di costruirle… lo dice Eulero!
Ecco a voi un esempio idiota di come cose complicate, con alla base tanti studi e teoria, possano essere prese e applicate – concedetemelo – con il culo, così da tirare fuori qualcosa di pseudoscientifico che è difficile da smontare per chi non è esperto dell’argomento.
In entrambi i casi, quello che abbiamo fatto è sbagliato: stiamo estrapolando dal contesto un solo elemento della struttura, trascurando tutto ciò che vi è collegato, e applicando una formula che descrive il comportamento della struttura nel suo complesso. In altre parole, è del tutto inutile modellare un pilastro delle Torri Gemelle senza considerare tutti gli altri pilastri e tutte le travi che li collegano. Allo stesso modo, non possiamo applicare l’instabilità di Eulero alla sola colonna vertebrale per il semplice fatto che non è da sola. Il vostro chirurgo ha finito di ricucirvi? Bene, ora chiedetegli quante difficoltà ha avuto nel rimettere a posto tutti i muscoli e i legamenti che aveva reciso per togliere la colonna vertebrale. Ecco la risposta. Ecco l’errore che facevamo.
Siamo arrivati alla conclusione. Abbiamo scoperto che Kapanji, o chi per lui, ha sbagliato a definire l’indice di resistenza perché l’ha derivato da una teoria che considera la rigidezza della struttura, ha sbagliato a non considerare la stabilità delle configurazioni di equilibrio perché tutte instabili (Eulero, 1755) e ha sbagliato ad applicare il modello decontestualizzando la colonna vertebrale dalla schiena.
Questa cosa della stabilità della colonna vertebrale, secondo me, è nata proprio da qui, e da allora continuiamo a parlarne un po’ a sproposito. Tutti gli studi successivi cercano di spiegare la stabilità della colonna, ma faticano ancora a trovare una configurazione di equilibrio che sia sensata. Ma se non si sa qual è la condizione di equilibrio, come si può valutarne la stabilità? Va beh, sono finezze che non importano a nessuno, e si andrà avanti a parlare di stabilità della colonna per sempre, ma l’evidenza è che nemmeno con 710 kg sulla schiena questa si instabilizza, anzi, ci si può fare una passeggiata. Perciò o il buon vecchio Brian Shaw viola le leggi della meccanica, o sarebbe meglio capire come modellare correttamente la colonna vertebrale prima di sparare minchiate.

Articolo a cura dell’Ing. Augusto Pedron, ingegnere civile strutturista, progettista di NERD TRAINING GEAR e istruttore strongman.